

BOOK REVIEW
The Volterra Chronicles: The Life and Times of an Extraordinary Mathematician 1860 – 1940, by Judith R. Goodstein, American Mathematical Society, Providence, 2007, 310 pages, ISBN: 978-0821839690
Reviewed by Irwin W. Sandberg 1,2


This book by Judith R. Goodstein, a Caltech archivist, is an imposing tribute to Vito Volterra, an exceptional mathematician, physicist, educator, statesman, and man of uncommon integrity. It is also an interesting, carefully written, richly-detailed history of his personal life and the times in which he lived. Much of the material was drawn from Volterra’s personal correspondence and from interviews with his family members. The book includes translations of actual correspondence, examples of which are given below, as well as several photos that help to round out the biography.
Samuel Giuseppe Vito Volterra was born into a Jewish family in Ancona, Italy’s Jewish ghetto in 1860 – during the period of the Italian unification and the year of the liberation of the Italian ghettos. His family was of modest financial means, and he had the misfortune that his father Abramo Volterra died when he was about two years old. For these reasons, he and his mother Angelica lived for most of Vito’s youth in the home of her brother Alfonso Almagià, first in Turin and later in Florence. Inspired by books he had read, Vito became interested in mathematics and science in his preadolescent years, to the dismay of both his mother and his uncle who, during Vito’s early teens, advocated a career in a more practical area such as railroad engineering or land surveying. Alfonso was an official at the Bank of Italy with a modest income that could not support Vito’s aspirations. Goodstein tells us that in a letter from Alfonso to his cousin Edoardo Almagià, Alfonso wrote “I make Vito come to the bank every day where I give him some work to do [in which he showed no interest, his uncle made clear] . . . God grant that he might overcome his disgust for anything that takes him away from his beloved science . . . That damned passion for the study of pure mathematics discourages me.”
As we know, Vito prevailed – this with the encouragement and assistance of Edoardo and others, including the physicist Antonio Ròiti in whom Vito found a scientific mentor and a person who shared his perspective on mathematics. Volterra’s geometry instructor at the Instituto Tecnico, the technical high school in Florence, was Cesare Arzelà during the years before Arzelà began his ascent on the academic ladder. During a class meeting, young Vito solved – on the spot – a problem put on the blackboard by an unannounced inspector from the Ministry of Public Instruction, after Arzelà, to whom the problem was addressed, appeared to be confused.
Volterra was eighteen when he left Florence to become a freshman at the University of Pisa. He took algebra from Cesare Finzi, a fine instructor and a family friend. His calculus class was taught by the brilliant and accomplished Ulisse Dini. In a letter to Vito’s mother, who had asked (earnestly) that her son write frequently, one finds:
-
Uncle asks how I like the lectures by Finzi. They are without doubt very beautiful lectures; he is a teacher who explains things with order and clarity, he never gets confused, he is sufficiently precise, speaks well and is also good and kind; one really could not ask for a better person to teach algebra. But I always prefer Dini, who gives lectures that are a bit confused, who some days explains and explains without reaching any conclusions and at other times is a bit obscure. I prefer him because he puts his whole soul into his lectures, because the things he explains are almost always his own discoveries – at least the method is really all his own. He speaks simply and gets a little confused but in the end his concepts are infinitely more clear, more concise, and, what is more important, more exact, than those of Finzi. Dini’s lectures are always interesting. (p. 39)
It is not surprising that it was Dini who inspired Volterra’s interest in pure mathematics. But Enrico Betti, a highly respected professor of mathematical physics and the director of the Pisa school of mathematics, had a strong interest in applications. It was he who served as Volterra’s dissertation advisor, and who provided the inspiration for Volterra to spend the rest of his career working, in an academic environment, on both pure mathematics and applications in the area of physics. Volterra was twenty-two years old when he graduated from the University of Pisa with a doctorate – not in mathematics, but in physics. By that time he had published five papers. Just one year later, in 1883 and after a competition with six other applicants, he became an associate professor at the University of Pisa – and held its Chair of Rational Mechanics. His promotion to full professor occurred in 1887, the year in which he was awarded a gold medal for mathematics from the Italian Society of Sciences. This medal was the first of his many awards and honors that later included membership in Italy’s prestigious Accademia dei Lincei (which translates to “Academy of Lynxes,” a name chosen by the academy’s founders in 1603 probably because the mythological lynx possessed piercing eyesight). Volterra initiated the powerful branch of mathematics that came to be called functional analysis, and made important contributions in several fields, including elasticity theory, the study of the movement of the earth’s axis of rotation, linear integral and differential equations, and later the theory of ecology and biology. He left Pisa in 1893 to accept a professorship in rational mechanics at the University of Turin.
From the perspective of modern mathematics the concept of a functional, while decidedly useful, is a natural and uncomplicated one. After it was introduced by Volterra in his 1887 paper “On functions that depend on other functions,” and developed further by him during the succeeding three years, it was rightfully viewed by Jacques Hadamard and others as a highly creative idea. In a classic 1945 essay, Hadamard wrote
-
. . . But that “functionals” as we called the new conception, could be in direct relation with reality could not be thought of otherwise than as mere absurdity. Functionals seemed to be an essentially and completely abstract creation of mathematicians.
-
Now, precisely the absurd has happened. Hardly intelligible and conceivable as it seems, in the ideas of contemporary physicists (in the recent theory of “wave mechanics”) the new notion, the treatment of which is accessible only to students already familiar with very advanced calculus, is absolutely necessary for the mathematical representation of any physical phenomenon . . . (p. 70)
Today, functional analysis, as developed much further by Banach, Fréchet, Hahn, and others plays an important role in the theory of stability of nonlinear automatic control systems, as well as in other areas of engineering and science such as system representation theory. In the stability studies one encounters, for example, Volterra integral equations of the form
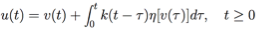
in which u and v are the system input and output, respectively, k is associated with the linear part of the system and η represents the nonlinear part.
While a faculty member at Pisa, Volterra served as an external examiner at a technical institute in Sicily where a student, upset by his failure to pass an exam proctored by Volterra, fired a pistol at him. Fortunately, the student’s marksmanship was no better than his performance on the exam: he missed. An interesting thread woven into Goodstein’s lively and richly detailed account of Volterra’s life and times concerns the disproportionately large number of Jews within Italy’s mathematics community. She notes, for example, that in 1895 Volterra received the Accademia dei Lincei’s mathematics prize (for “various memoirs on pure and applied analysis”), that the co-winner Corrado Segre, the leader of the Italian school of geometry, was also from a Jewish background, and that, by the time of the collapse of the academy under Mussolini in 1944, seven of the sixteen prize winners in mathematics were Jewish. These Jewish prize winners included Guido Castelnuovo and Federigo Enriques (both known for their contributions in the area of algebraic geometry), as well as Guido Fubini (of Fubini’s theorem). The population of Jews in Italy at that time was a tiny fraction of one percent.
When he was about forty, Volterra’s mother decided that the time had come for him to marry, and she proceeded to arrange a marriage. His bride was to be the much younger Virgina Almagià, his second cousin and the daughter of Alfonso Almagià whose modest railroad construction business had grown into a large international engineering company. Virgina was educated, intellectually brilliant, and a lovely young woman. Vito’s main concern appears to have been that he did not want to be thought of as one who married for money. He sought advice from his mentor Antonio Ròiti who wrote
-
. . . It is therefore necessary to think seriously before taking a very rich wife. I must confess that I have always felt a strong repugnance for this. To give you my opinion without any hesitation, I need to know the education, aspirations, and habits of this young lady and the kind of life she will have to lead to be fully happy after she has been married for many years. To have an idea of all this, it is necessary to talk to you. For now, I can say at once with a clear conscience that although on one side there is great wealth, on the other side, given your intelligence, your industriousness, and universal esteem you enjoy, no one who has any sense will deny that your social position is already much more brilliant and admirable than that of a person who has millions. Thus, an open minded woman with noble feelings – however rich – should feel honored and elevated by your choice. (p. 107)
There were other considerations too, but in the summer of 1900 Virgina and Vito were married. That year he accepted the mathematical physics chair at the University of Rome where he would stay for more than thirty years. It was no accident that Virgina’s parents lived in Rome, but from all accounts Volterra’s marriage was a highly successful one. In the ensuing twenty years Volterra’s professional stature grew immensely. He traveled extensively and lectured in France, England, Norway, Sweden, and the United States, and was received as a widely respected mathematician of the first rank.
In Italy, he became a Senator of the Kingdom, a lifetime position in the upper house of parliament where he participated in many of its deliberations. In an early speech to the Italian Senate he called for a revamping of Italy’s advanced technical school system, actually arguing that too much mathematics was taught. In his role as a politician, he cited Alois Riedler, a German professor of mechanical engineering, who had said that “an excess of mathematical and theoretical studies not only is useless and takes up precious time, but is absolutely pernicious to the engineer, impairing the education of the spirit.” Of course Volterra who had become Italy’s leading mathematician, and who pressed for a better balance in engineering education, continued to be a powerful advocate of mathematics in general. Goodstein tells us that Riedler reminded Volterra “not a little of Attila the Hun.”
Volterra knew Felix Klein, Hermann Schwarz, Georg Cantor, as well as many other notable mathematicians of his day, and he developed a particularly friendly relationship with the Swedish mathematician Gösta Mittag-Leffler, a former student of Karl Weierstrass. Volterra spent several days in Wernigerode with Weierstrass and the famous Russian mathematician Sofia Kovalevskaya who then was a chaired professor at the the University of Stockholm. She too had been a student of Weierstrass. Goodstein relates to us that Mittag-Leffler had met Sofia years earlier and commented to a Swedish associate:
-
. . . as a woman, she is fascinating. She is beautiful and when she speaks, her face lights up with such an expression of feminine kindness and highest intelligence, that it is simply dazzling . . . She is in all respects a complete “woman of the world.” As a scholar she is characterized by her unusual clarity and precision of expression . . . I understand fully why Weierstrass considers her the most gifted of his students. (p. 72)
The book contains a photo of Kovalevskaya.
Goodstein’s last chapter begins with an account of the role Volterra played during the first world war, with some emphasis on his work concerning the firing of canons aboard hydrogen-inflated dirigibles. This account is not uninteresting, but the most compelling part of chapter concerns Volterra’s final years. The cancer that was Mussolini’s fascism – together with Mussolini’s pacts with Nazi Germany, a regime marked by its rabid anti-Semitism – brought down the Italian golden age of mathematics and science. Volterra was dismissed from his university position and ceased to belong to Italian scientific societies because he refused to sign an oath of allegiance and devotion to the Fascist regime (only eleven other professors in all of Italy refused). Italy’s subsequent so called “racial laws” dictated that Jews could not attend public schools or universities, work as journalists, teachers, or notaries, or even use libraries. Volterra died of natural causes in 1940 in such obscurity that three years later, when Rome was occupied by the Nazis, German soldiers actually arrived at the house he had lived in expecting to deport him to a concentration camp. Virgina survived the Nazis with the help of the family’s librarian who hid her until a more secure place was found with a group of nuns.
Virgina and Vito had six children, but sadly only four lived to become adults. One became a distinguished judge. Their son Enrico earned a Ph.D. at Cambridge University and taught at the University of Texas at Austin where he was a professor of aerospace engineering. Their daughter Luisa married Umberto D’Ancona, a marine biologist who was the supervisor of her undergraduate thesis at the University of Rome. It was D’Ancona who sparked Volterra’s interest in the mathematical study of population dynamics in the Adriatic.
The biography contains three appendices: transcripts of two of Volterra’s talks, and an obituary containing a description of Volterra’s contributions to mathematics by Sir Edmund Whittaker. Outlines in English of Volterra’s life have been available since the 1940s, but for an outstanding account of the life and times of Volterra this is the biography to read.

1 Irwin W. Sandberg is Cockrell Family Regents Chair Emeritus in Engineering at the University of Texas at Austin, USA. His e-mail address is sandberg@ece.utexas.edu.
2 This review was first published in the Notices of the American Mathematical Society in March 2008, published by the American Mathematical Society.
